Let's have a look.
Intuition
The idea behind it is to divide the array to sort into two sub-arrays: the first that contains the sorted data and occupies the first positions of the array while the second contains the data that have to be sorted and it occupies tendentially the final positions of the array. At the beginning, the subsequence of sorted elements is empty while the subsequence that represents the unsorted elements occupies the entire array..
The algorithm chooses at every iteration the minimum in the unsorted sequence and puts it into the sorted subsequence. The procedure goes on until the sequence of unsorted elements is not empty.
Let's watch this GIF:
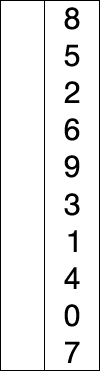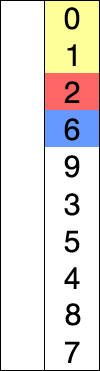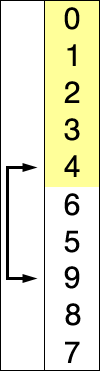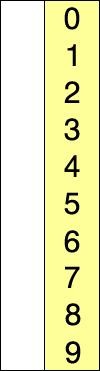
Flow-chart
Let's analyze the algorithm's flow-chart, gently given by GeeksforGeeks.com.
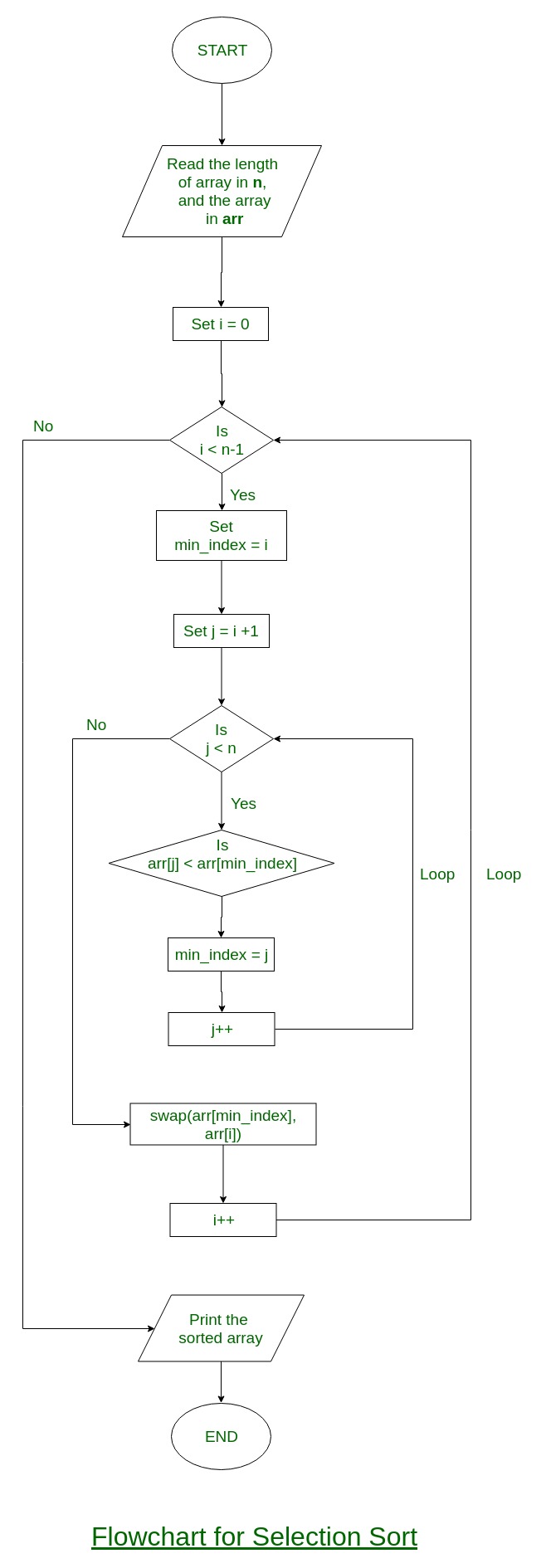
There are two basic cycles that implement the whole procedure. The first cycle is used to keep track of the position in which to insert the minimum that we have found while the second is used to find the minimum within the collection.
Implementation
Let's have a look to the implementation of the algorithm.
// Java program for implementation of Selection Sort
public class SelectionSort
{
public static void sort(int arr[]) {
int n = arr.length;
for (int index = 0; index < n-1; index++)
{
// find the minimum element within an unsorted array
int min_idx = index;
for (int j = index+1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
// swap the minimum with
// the current element
int temp = arr[min_idx];
arr[min_idx] = arr[index];
arr[index] = temp;
}
}
public static void main(String args[]){
int arr[] = {64,25,12,22,11};
System.out.println("Unsorted array");
System.out.println(Arrays.toString(arr));
SelectionSort.sort(arr);
System.out.println("Sorted array");
System.out.println(Arrays.toString(arr));
}
}
Let's understand the code
I made the sorting method static, like in the previous examples. The first cycle is used to keep track of the current position of the array while the innermost cycle is used to search for the minimum.
The search for the minimum must be sequential, as there are no preconditions for being able to carry out a dichotomous search, for example.
Now, we are going to analyze better the cycles that compose the algorithm
- outer cycle from 0 to arr.length-1: this loop keep track of the effective iterations of the procedure, also allowing to trace the position where the new found minimum will be placed. The "interesting" thing is that it iterates to the penultimate position of the vector. The motivation is somewhat trivial. When you reach the last position, there are no more elements to exchange it with, so it is useless to make an extra turn. It is sufficient to stop at the penultimate position;
- inner cycle: this cycle is used to search for the minimum in a portion of the array, more specifically from index+1 to arr.length-1. Unlike the external loop, here we also examine the last position as it is a possible candidate as a minimum. We do not store the value of the minimum but rather the index that we will then need for the exchange.
At the end there is the exchange procedure, on which it is worth spending a few words.
To a novice eye, the variable named temp may seem unnecessary. On the contrary, it is indispensable, because it allows us not to lose the value of one of the two variables after the first assignment operation. In fact, first we save the value of array [min_idx] in temp, then we place it in array [min_idx] array [index [and finally in array [index] we place temp. In this way two variables are exchanged correctly.
Recursive implementation
// Recursive Java program to sort an array
// using selection sort
public class RecursiveSelectionSort
{
// returns the index of the minimum
static int minIndex(int a[], int index, int j)
{
if (index == j)
return index;
// find the minimum among the remaining elements
int k = minIndex(a, index + 1, j);
// Return minimum of current and remaining.
return (a[index] < a[k])? index : k;
}
// recursive Selection sort. n is the length of a[] and index
// is the index of the starting element.
public static void recurSelectionSort(int a[], int n, int index)
{
// Return when starting and size are same
if (index == n)
return;
// calling minimum index function for minimum index
int k = minIndex(a, index, n-1);
// swap when index and the index of the minimum are not the same
if (k != index){
// swap
int temp = a[k];
a[k] = a[index];
a[index] = temp;
}
// recursively call the method for the selection sort
recurSelectionSort(a, n, index + 1);
}
public static void main(String args[])
{
int arr[] = {3, 1, 5, 2, 7, 0};
System.out.println("Unsorted array");
System.out.println(Arrays.toString(arr));
// call the function
recurSelectionSort(arr, arr.length, 0);
System.out.println("Sorted array");
System.out.println(Arrays.toString(arr));
}
}
Let's understand the code
This algorithm is quite well suited for a recursive implementation. Let's analyze it better.
- minIndex method: it has as parameters the left and right limit within which it is necessary to research the minimum. The base case is when the end of the not examined elements has been reached, so it returns the current index. The last instruction is used to compare a[index] and a[k] and to return the index of the minimum between them.
- recurSelectionSort method: the method has the array to sort and two integer numbers as parameters. The two numbers represent the length of the array and the position that we are examining. The procedure is the same of the iterative version. We found the minimum and we swap it with the current position. The minimum is found recursively as explained before. Instead of a loop, we use a recursive implementation to be able to scroll through the array. In fact, after making the exchange, the method is called recursively, but by increasing the index parameter, which represents the current position within which to put the minimum.
The main is the same as the previous, where we pass as parameters the array to sort, its length and 0 (the starting index).
Complexity
The internal cycle is a simple test to compare the current element with the minimum element found so far (plus the code to increase the index of the current element and to verify that it does not exceed the limits of the array). The movement of the elements is out of the internal cycle: the number of exchanges is equal to (since the last element must not be exchanged). Calculation time is determined by the number of comparisons.
The sort by selection makes comparisons and, in the worst/best/average case, exchanges.
The complexity of such algorithm is of

 (since the last element must not be exchanged). Calculation time is determined by the number of comparisons.
(since the last element must not be exchanged). Calculation time is determined by the number of comparisons. comparisons and, in the worst/best/average case,
comparisons and, in the worst/best/average case,  exchanges.
exchanges.