Java Sorting Algorithms: Merge Sort

Today we are going to analyze one of the most used sorting algorithms: the Merge Sort. It is part of the Divide and Conquer family, just like the  Quick Sort. Merge Sort offers a better performance despite of the Quick Sort since its complexity remains O(n log n) keeping performances. It is also called "algorithm by fusion"

The main defect of the Merge Sort is that it needs auxiliary data structures in order to execute its tasks. We can say that it is a stable and adaptive algorithm, but it is not in-place.

How does it work?

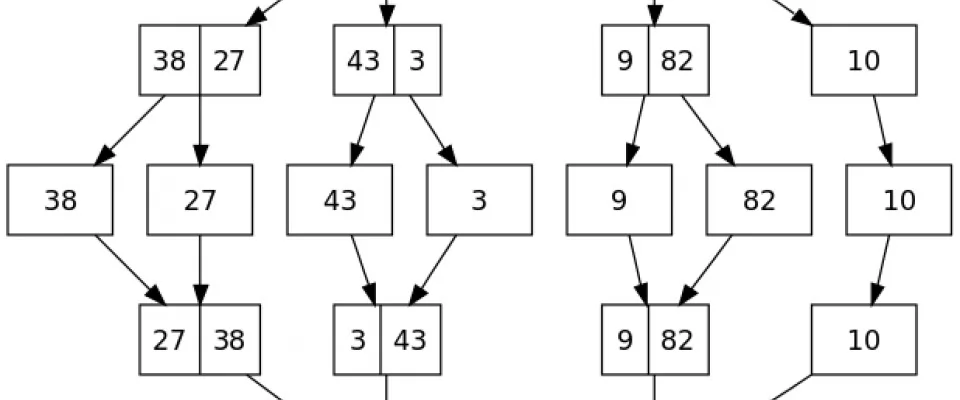
Let's start looking at an image that explains very well how the algorithm works.

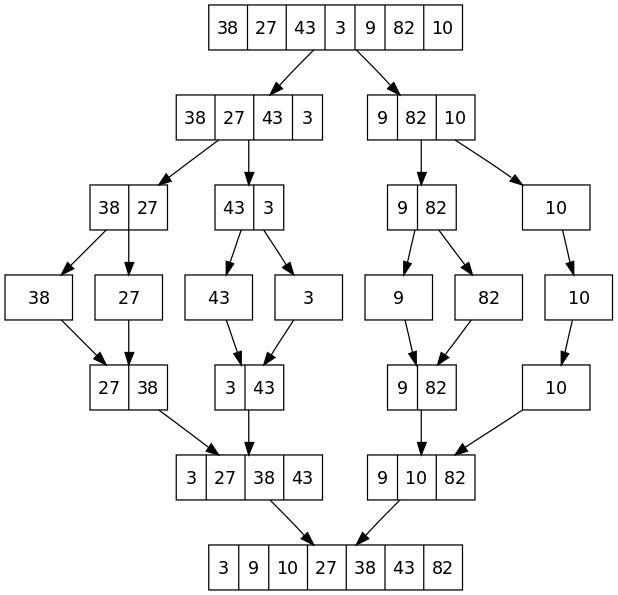
If someone has already had to deal with large collections of data to order, the way of working of the algorithm may be already known. The basic idea is the one of dividing the array into small groups and sort them. Once the sorting operation of every subset is completed the minimum element among the elements is taken and it is put into the final array. The process is repeated until every subset contains at least one element.

The foundamental problem is the fusion process.

Fusion algorithm

• The left half of the array is copied on an auxiliary array;
• The minimum element between the auxiliary array and the right half of the array is chosen and the value is copied on the final array;
• The process ends when every element of the auxiliary array has been copied;

Implementation

public class MergeSort 
{ 
    // Merge the two half of arr[]. 
    // The first subset of the array is arr[l..m] 
    // The second subset of the array is arr[m+1..r] 
    public static void merge(int arr[], int l, int m, int r) { 
        // Find the size of the two subarrays to merge
        int n1 = m - l + 1; 
        int n2 = r - m; 

        /* Create auxiliary arrays */
        int L[] = new int [n1]; 
        int R[] = new int [n2]; 

        /*Copy data to auxiliary arrays*/
        for (int index=0; index<n1; ++index) 
            L[index] = arr[l + i]; 
        for (int j=0; j<n2; ++j) 
            R[j] = arr[m + 1+ j]; 

        /* Merge the auxiliary arrays */

        // Starting indexes of the two arrays
        int index = 0, j = 0; 

        // Starting index of the final array
        int k = l; 
        while (index < n1 && j < n2){ 
            if (L[index] <= R[j]) { 
                arr[k] = L[index]; 
                index++; 
            } else{ 
                arr[k] = R[j]; 
                j++; 
            } 
            k++; 
        } 
        /* Copy the remaining elements of L[] if any */
        while (i < n1) { 
            arr[k] = L[i]; 
            index++; 
            k++; 
        } 

        /* Copy the remaining elements of R[] if any */
        while (j < n2) { 
            arr[k] = R[j]; 
            j++; 
            k++; 
        } 
    } 

    // Main function that sorts arr[l..r] using 
    // merge() 
    public static void sort(int arr[], int l, int r) { 
        if (l < r) { 
            // Find the middle point
            int m = (l+r)/2; 

            // Sort the first and the second half
            sort(arr, l, m); 
            sort(arr , m+1, r); 

            // Merge the two halves
            merge(arr, l, m, r); 
        } 
    } 

    public static void main(String args[]) { 
        int arr[] = {12, 11, 13, 5, 6, 7}; 

        System.out.println("Unsorted array"); 
        System.out.println(Arrays.toString(arr));

        MergeSort.sort(arr, 0, arr.length-1); 

        System.out.println("Sorted array"); 
        System.out.println(Arrays.toString(arr));
    } 
} 

Let's understand the code

First of all, some precisation. When we write a for cicle we can omit the curly brackets if the body of the cicle contains only one instruction. In this case, in the two for cicles written above the curly brackets can be omitted since there is a single instruction and there will not be any problem about the extension of the code.

Like in the example about Quick Sort I made static methods since I think that it is useless using non-static methods. Non-static methods would need an object that would call them and this object would have to be created and managed.

• Merge method:
  
  The two halves' sizes are calculated and then the arrays are created. After that, the two subsets of the starting array are copied to the auxiliary structures. At the end the elements are sorted and copied to the original array again.
   
• Sort method
  
  In this method the medium point of the array is calculated. This point is used to make the division into subarrays. Using the middle point is important in order to balance the complexity of each call. Then the two halves, respectively of indexes (l, m) and (m+1, r) are sorted. 
  At the end the two parts are merged.
  The most important thing is the check on l and r. These two indexer represent the two limits of the array to sort. L stands for the left limit while R stands for the right limit. The problem is that, under particular conditions, l could become greater then r. This could create inconsistent situations so the necessary condition for the execution of the entire procedure is l < r, thus avoiding errors in passing parameters and inconsistencies in situations. 
   
• Main
  
  This main is quite easy. The collection to sort is created (in this case the collection is an array composed of integer numbers). The sort methodo is then called passing the array to sort, 0 and n-1 (where n-1 stands for the array's length) as parameters.
  The right extreme is the index of the last element of the array because the algorithm iterates in a range of the type [ 0 ; array.length ), that can be written equivalently as  [ 0 ; array.length-1 ], simplifying the controls in the various cycles.

Mentions about complexity

Complexity of the fusion process

The complexity of the merging process has a linear growth, in fact at each iteration the final array's size always grows by 1. So it is O(N).

There is starting cost of O(N) for the copy of the auxiliary array.

Algorithm cost

T(n) = 2T(n/2) + 

Through suitable algebraic passages it is possible to reach the conclusion that the complexity of the algorithm is equal to .

When can Merge Sort be useful?

Merge Sort can be useful expecially when we deal with Linked Lists just because the insertion process has linear complexity. Because the nodes of the list are not adjacent, it is particularly convenient to use this algorithm. This is the most significant situations, but this is not the only one.

Alessio Mungelli

Computer Science student at UniTo (University of Turin), Network specializtion, blogger and writer. I am a kind of expert in Java desktop developement with interests in AI and web developement. Unix lover (but not Windows hater). I am interested in Linux scripting. I am very inquisitive and I love learning new stuffs.