In this short series of articles we will go to see how it is possible to create the Hashmap data structure in C.
In the implementation we're going to use the doubly concatenated lists as auxiliary data structures. Let's look at a possible implementation.
Header file
Let's first have a look to what the .h file looks like.
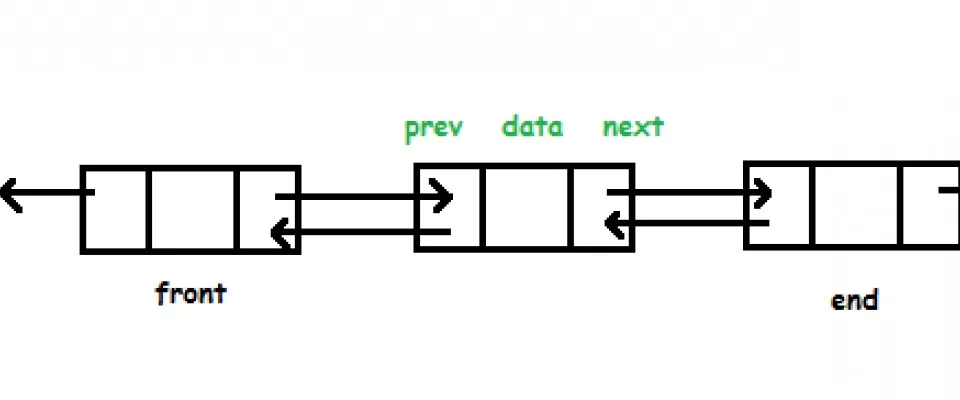
Definition of a node
We define the node data structure as follows:
typedef struct node_t{
struct node_t *prev;
struct node_t *next;
void *data;
void *key;
}node_t;
We are therefore defining a new node_t data type. This new structure is composed of 4 fields:
- prev, which represents the predecessor of the node in the list;
- next, which represents the next node in the list;
- date, which is the information represented by the node;
- key is instead the node's identification key;
Both key and date fields have been declared as pointers to void as the idea is to make generic code that can be used under any circumstances.
Definition of the list data type
The list will have a definition like:
typedef struct overflow_list{
node_t *head;
node_t *tail;
} overflow_list;
The idea is to keep a pointer at the head of the list and also at the tail, in order to perform the head and tail entries in constant time.
Other useful definitions
It will be useful to make these two typedef.
typedef int (*CMPFUNC)(const void *, const void*); typedef void (*PRNTFUNC)(const void *);
The first definition states a function pointer that I call CMPFUNC which has two void pointers as parameters. This function will be used later on to compare the two parameters which, in the real implementation, will have well-defined types.
The PRNTFUNC declaration is used to declare the type of a function that prints a pointer. It is necessary because the application I have created prints on the command line of printf, which is why we need to know what type the data you want to print is.
All the functions whose implementation I will provide must have a corresponding statement in the header file.
Function implementation
Creazione di un nodo
The first thing we need is a convenient function to create a new node.
node_t *create_node(void *k, void *d){
node_t *n = (node_t*)malloc(sizeof(node_t));
n -> data = d;
n -> key = k;
n -> next = NULL;
n -> prev = NULL;
return n;
}
create_node takes as parameter two pointers to void k and d which represent the key and the data stored in the node respectively. After executing the malloc to allocate the necessary space, we assign the parameters to the respective fields of the newly created node_t. The next and prev fields are set to NULL as the node has not yet been entered in the list, so we still don't know what value those two fields will have.
Creating a list
overflow_list *create_empty_doubly_linked_list(){
overflow_list *l = (overflow_list*)malloc(sizeof(overflow_list*));
l -> head = NULL;
l -> tail = NULL;
return l;
}
This function acts as a "constructor" for the list, allocating the list space and setting both the tail and the head to NULL.
The reason, however trivial, is that an empty list contains no elements, so the two fields will be null.
Inserimento di un elemento nella lista
void insert_item(overflow_list *l, void *k, void *v){
node_t *n = create_node(k, v);
if(l->head == NULL){
l->head = l->tail = n;
}else{
l->tail->next = n;
n->prev = l->tail;
l->tail = n;
}
}
The important thing to understand is the meaning of the parameters. The list l represents the list within which we want to make the insertion. The k and v fields are the data that will be stored in the node we will insert. Here we do not worry about the presence or absence of duplicates in the collection. Later on we will see a way to avoid the insertion of duplicate elements.
The algorithm is that of queued entries, which can be done in constant time by keeping and updating the pointer at the list queue.
Search for a key
We want to create a function that tells us whether or not an item is present in a list by making a comparison on the keys.
node_t *contains_key(node_t *head, void *k, CMPFUNC compare){
while(head!=NULL && compare(k, head->key) != 0){
head = head->next;
}
return head != NULL ? head : NULL;
}
The idea is to scroll through the list until you find the item in question or the list items are finished.
We need the comparison function to appear as we cannot directly compare two pointers to void. At the end of the method we return the pointer to the node we found if NULL is not valid. We return NULL otherwise.
Removing an element
To implement the removal, I have defined two auxiliary functions that take care of removing the element from the head or tail.
Head Cancellation
Let's see the delete algorithm from the head of a list.
void remove_from_beg(overflow_list *l){
node_t *temp;
if(l->head == NULL){
printf("Trying to delete from empty listn");
}else{
temp = l->head;
l->head = l->head->next;
if(l->head!=NULL){
l->head->prev = NULL;
}
temp->next=NULL;
free(temp);
}
}
The only thing to do is to update the pointer at the top of the list. I found it useful to store the node that is disconnecting from the list so that I can call up the free on that node.
You update the pointer to the head by enhancing it with its next element and set the prev field of the new head to NULL.
Queue cancellation
void remove_from_end(overflow_list *l){
node_t *temp;
if(l->tail==NULL){
printf("Trying to delete on empty listn");
}else{
temp = l->tail;
l->tail->prev->next = NULL;
l->tail = temp->prev;
free(temp);
}
}
L'idea è similare a quella della rimozione in testa, con l'unica differenza che si aggiorna il puntatore alla coda con il suo precedente.
Anche questa operazione viene eseguita in tempo costante.
Cancellation in any position
void remove_item(overflow_list *l, void *k, CMPFUNC compare){
node_t *temp = contains_key(l->head, k, compare);
if(temp == l->head){
remove_from_beg(l);
}else if(temp == l->tail){
remove_from_end(l);
}else{
if(temp!=NULL){
if(temp->prev!=NULL){
temp->prev->next = temp -> next;
}
if(temp->next!=NULL){
temp->next->prev = temp->prev;
}
free(temp);
}
}
}
This function combines the two functions written before, adding the removal of an element that is not at the top and the bottom.
So if the item you want to remove is the head or tail of the list, you call up the appropriate functions. If the item is central, we disconnect it from the list as shown in the image below.
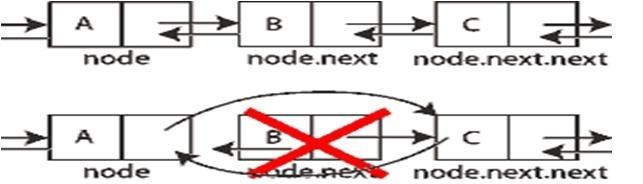
The idea is therefore to "unlink" the knot, thus removing it from the list, then sewing the links so as not to unlink the list.
Search
Having a data structure, research operations are indispensable to say the least.
We will see two implementations: one iterative and one recursive.
Key search
node_t *contains_key(node_t *head, void *k, CMPFUNC compare){
while(head!=NULL && compare(k, head->key) != 0){
head = head->next;
}
return head != NULL ? head : NULL;
}
The fundamental idea is to look for a knot in a list, scrolling the knots one by one starting from the head.
The while guard has this meaning: the cycle continues to iterate until the node we are examining is equal to NULL and until the comparison function gives us a value other than zero when comparing the parameter k and the key of the current node.
At the end the value of the head parameter will be returned.
Search for a data
The principle of searching for data is exactly the same as that of searching for the key. However, the following implementation is recursive.
node_t *contains_data(node_t *head, void *d, CMPFUNC compare){
if (head == NULL){
return NULL;
}
else if (compare(head->data, d)==0){
return head;
}
else{
return contains_data(head->next, d, compare);
}
}
General scheme of scrolling through a list
In the search operations the scheme for scrolling the list is always the same, and it is the same every time you have to do operations that require scrolling the structure.
Let's see briefly what it is.
void run_through(overflow_list *l){
node_t *temp = l -> head;
while (temp != NULL) {
temp = temp -> next;
}
}
We have a temp node that acts as a cursor. In the cycle, the instruction temp = temp -> next uses the node's next field to scroll through the various nodes.
In the next articles we'll look at how to use double-linked lists to implement hashmaps.