Programming, the need to order the collections of data or objects that must then be manipulated often arises. Ordering a list can be useful in cases where you have to do very quick searches. We will see later on how to maintain an ordered list is useful to carry out dichotomous searches and therefore have the results in a clearly lesser time compared to a sequeial search.
In this article we will refer to arrays composed of integer numbers. The algorithm is the same for every data type.
Algorithms' property
This is a speech that I do now and it is the same for every algorithm that we will study in the next articles.
Generally, every algorithm has properties that are useful in order to study them and above all, usefull to decide what algorithm is the best for the situation that is been considered. Let's see better.
Stability
An algorithm is called stable if it preserves the relative order of the data with identical keys within the file to be ordered. For example, if we are looking at a list of people sorted in alphabetical order, a stable algorithm will always return an ordered list in alphabetical order. If the algorithm were unstable, a list would be obtained without any trace of the previous ordering.
A possible way to force the stability of an algorithm is the one of adding a unique key for every element. This principle is similar to one rule of database design.
In-place
An algorithm is called in-place if it uses a constant number of variables to sort the array and it doesn't uses auxiliary arrays.
Adaptivity
An algorithm is called adaptive it if gains advantage from the elements that are already sorted.
Let's analyze better some implementations of a sorting algorithm: the Bubble Sort.
Bubble Sort
The Bubble Sort is a sorting algorithm that is not very efficient. It is often used for educational pourposes to introduce the concept of sorting algorithm.
Why "bubble sort"?
The algorithm's name comes from its behavior. In fact the elements of the vector behave exactly like the bubbles in a glass of champagne: the larger ones rise upwards while the smaller ones remain at the bottom, exactly as shown in the gif below.

Flow-chart
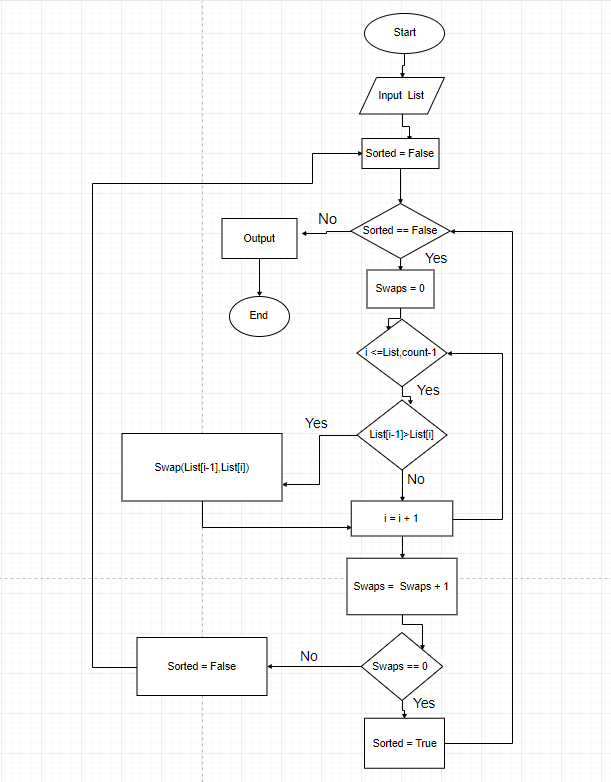
Implementation
The flow-chart shows an optimized version of the algorithm, while the code shown below presents the classic version.
public static void bubbleSort(int[] v) {
int n = v.length;
int temp = 0;
for(int index=0; index < n; index++){
for(int j=1; j < (n-index); j++){
if(v[j-1] > v[j]){
//swap elements
temp = v[j-1];
v[j-1] = v[j];
v[j] = temp;
}
}
}
}
This iterative implementation shows the exact procedure shown in the gif. In fact, printing step by step the various states of the array during the sorting process, we obtain:
[6, 5, 3, 1, 8, 7, 2, 4]
[5, 3, 1, 6, 7, 2, 4, 8]
[3, 1, 5, 6, 2, 4, 7, 8]
[1, 3, 5, 2, 4, 6, 7, 8]
[1, 3, 2, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]
Notiamo come il numero di passaggi che si devono fare per ordinare un array relativamente piccolo come quello dell'esempio sia veramente alto. Proprio per questo il bubble sort viene utilizzato fondamentalmente a scopi didattici a causa della sua inefficcienza. Proprio grazie alla predisposizione all'uso didattico, andiamo a fornire un'implementazione ricorsiva dello stesso algoritmo, definendo con swap il metodo che scambia due posizioni di uno stesso array.
We can notice that the number of iterations needed to sort a short array like the one shown above is very high. Because of this the Bubble Sort is used basically for educational pourposes because of its inefficiency. Thanks to the predisposition to didactic uses, we are now going to provide a recursive implementation of the same algorithm, defining with swap the method that exchanges two positions of the same array.
//recursive method to implement bubble sort on a subarray
public static void bubbleSort(int[] v, int n)
{
for (int index = 0; index < n - 1; index++) {
if (arr[index] > arr[index + 1]) {
swap(arr, index, index + 1);
}
}
if (n - 1 > 1) {
bubbleSort(arr, n - 1);
}
}
The obtained result is the same, but the way it is realized changes.
Properties
Carrying on the speech about the properties done before, we can try to identify what are bubble sort's properties.
The Bubble Sort is stable, in fact it always returns an array sorted in ascending or descending order regardless of the data in the collection.
It is also in-place since it doesn't uses and addictional arrays for the sorting operations.
It is also adaptive, in fact when the elements are sorted, the algorithm doesn't perform any operation and keep them sorted. This feature saves a considerable number of iterations.
Complexity
Making a more mathematical speech, let's see something about the complexity of the algorithm. Let's make a small introduction. Complexity is indicated by the so-called Landau symbols, used to compare the progress of two functions. In fact, we tend to associate the complexity of an algorithm with a function, to then compare it to a note.
Assuming that the complexity of a single swap is O(1), the complexity of the algorithm is given from the nested for cycles.
In the worst case we have a complexity of T(n)=n(n-1)/2 —> O(N²) while in the best case the array is already sorted and the number of iterations is 1.
On average, it performs around N2 / 2 comparisons and as many exchanges.
Optimizations and conclusions
A first way to optimize the algorithm is based on the fact that if in a certain iteration n no swaps are done, the array is sorted and then the algorithm can end. We use a boolean variable that check this condition. This kind of optimization is the one shown in the flow-chart above.
A second line of thought argues that if a given iteration does not move any element of position greater than a given value i, then you can easily demonstrate that no subsequent iteration will perform swaps in positions subsequent to that value i. The optimization consists in storing the index where the last exchange took place and scanning the array up to that value location. Even this technique obviously introduces a small overhead.
Ending the speech, we can say that the algorithm is very suitable for educational pourposes as I said before. It is not very suitable for sorting big arrays.
Spezzando una lancia a suo favore, è facile da capire e implementare, non richiede un grande ammontare di memoria e la cosa più importante è che, una volta finito l'ordinamento, i dati sono pronti per l'elaborazione.
But it has also some good points. In fact it is easy to understand and implement, it does not require a large amount of memory and the most important thing is that, once the sorting is finished, the data is ready for processing.

