Andiamo oggi ad analizzare uno tra i migliori algoritmi di ordinamento: il Merge Sort. Detto anche algoritmo per fusione, fa parte della famiglia dei Divide and Conquer proprio come il Quick Sort. A differenza del prima citato Quick Sort, il Merge Sort offre prestazioni migliori, siccome nella peggiore delle ipotesi la sua complessità rimane simile a O(n log n) mantenendo prestazioni ottimali.
L'unica pecca del Merge Sort è che necessita di strutture dati aggiuntive per poter svolgere le sue elaborazioni. Possiamo quindi dire che è un algoritmo stabile, ma non in-place. Inoltre è adattivo.
Funzionamento
Iniziamo guardando un'immagine esplicativa del funzionamento dell'algoritmo.
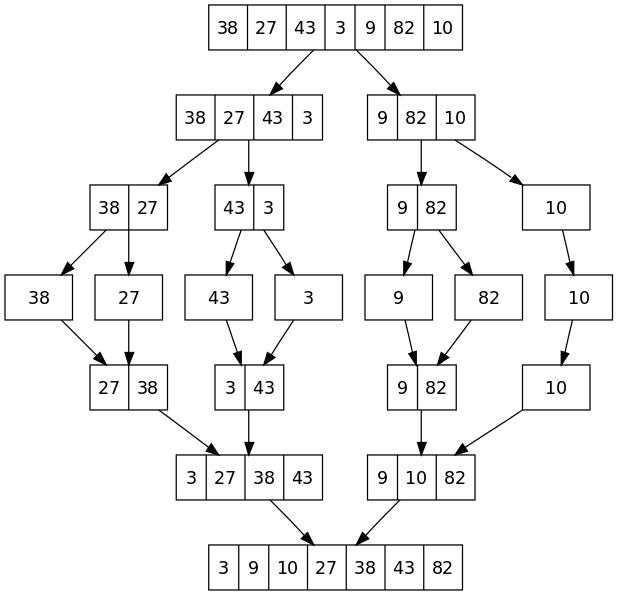
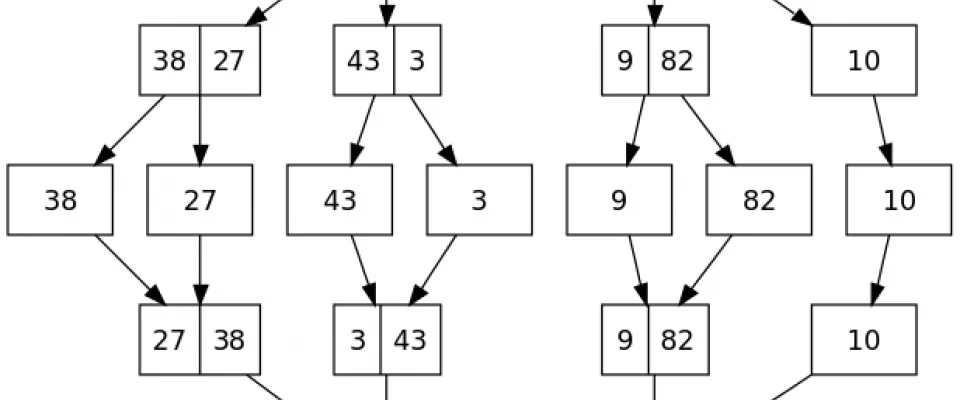
Il funzionamento potrebbe essere già noto a chi ha già avuto a che fare con grandi collezioni di dati da ordinare. L'idea alla base è quella di dividere l'array in gruppetti e ordinarli. Una volta finita l'operazione di ordinamento dei singoli sottoinsiemi si prende il più piccolo tra gli elementi dei vari gruppi e inserirlo nel nuovo array. Si itera quindi questo processo sino ad esaurimento dei "mucchietti".
Il problema fondamentale è la fusione.
Algoritmo di fusione
- Il semi-vettore sinistro è copiato su un vettore di appoggio;
- Si seleziona il minimo tra il vettore di appoggio e il semi-vettore di destra e lo si copia sul vettore finale;
- Si termina quando tutti gli elementi di appoggio sono stati copiati;
Implementazione
public class MergeSort
{
// Fonde due sottoarray di arr[].
// il primo sottoarray è arr[l..m]
// il secondo sottoarray è arr[m+1..r]
public static void merge(int arr[], int l, int m, int r) {
// Trova le dimensioni dei due sottoarray da unire
int n1 = m - l + 1;
int n2 = r - m;
/* Crea array temporanei */
int L[] = new int [n1];
int R[] = new int [n2];
/*Copia i dati in array temporanei*/
for (int index=0; index<n1; ++index)
L[index] = arr[l + i];
for (int j=0; j<n2; ++j)
R[j] = arr[m + 1+ j];
/* Unisce gli array temporanei */
// Indici iniziali dei due array
int index = 0, j = 0;
// Indice iniziale del sottoarray finale
int k = l;
while (index < n1 && j < n2){
if (L[index] <= R[j]) {
arr[k] = L[index];
index++;
} else{
arr[k] = R[j];
j++;
}
k++;
}
/* Copia gli elementi rimanenti di L[] se ce ne sono */
while (i < n1) {
arr[k] = L[i];
index++;
k++;
}
/* Copia gli elementi rimanenti di R[] se ce ne sono */
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
// Funzione principale che ordina arr[l..r] usando
// merge()
public static void sort(int arr[], int l, int r) {
if (l < r) {
// Trova il punto medio
int m = (l+r)/2;
// Ordina la prima e la seconda metà
sort(arr, l, m);
sort(arr , m+1, r);
// Unisce le due metà
merge(arr, l, m, r);
}
}
public static void main(String args[]) {
int arr[] = {12, 11, 13, 5, 6, 7};
System.out.println("Array da ordinare");
System.out.println(Arrays.toString(arr));
MergeSort.sort(arr, 0, arr.length-1);
System.out.println("nArray ordinato");
System.out.println(Arrays.toString(arr));
}
}
Capiamo il codice
Alcune note. Nei for è possibile omettere le parentesi graffe nell'eventualità che il corpo del ciclo contenga una sola istruzione. In questo caso, nei due for di copia dei dati nelle strutture temporanee è possibile omettere le parentesi graffe proprio perchè l'istruzione è una sola e non si presentano problemi relativi ad un eventuale ampliamento del codice.
Come nel Quick Sort ho reso i metodi statici in quanto non trovo utile utilizzare metodi dinamici che comporterebbero l'onere della creazione e gestione di un oggetto che li gestisca.
- Metodo merge:
Vengono calcolate le dimensioni dei due sottoarray e successivamente vengono istanziati. Dopodichè i due subset dell'insieme di partenza vengono copiati nelle due strutture ausiliarie. Dopodichè, riordina gli elementi rimettendoli nell'array originario.
- Metodo sort
In questo metodo viene calcolato il punto medio del vettore che servirà per effettuare la divisione in sottoarray. E' importante utilizzare il punto medio per bilanciare il carico di elaborazione di ciascuna chiamata. Dopodichè vengono ordinate le due metà dell'array, rispettivamente di estremi (l, m) e (m+1, r).
Infine vengono unite le due metà ordinate.
La cosa importante è il controllo su l ed r. Questi due indici rappresentano i due estremi dell'array da ordinare. L indica l'estremo sinistro ed R l'estremo destro. Il problema è che, sotto particolari condizioni, l potrebbe diventare maggiore di r. Questo potrebbe creare situazioni inconsistenti e quindi si pone come condizione necessaria per l'esecuzione dell'intero procedimento l<r, evitando così al contempo errori di passaggio dei parametri e inconsistenza delle situazioni.
- Main
Questo main è piuttosto semplice. Viene infatti creata la collezione di dati da ordinare (un array di numeri interi in questo caso). Viene quindi richiamato il metodo sort passando come parametri l'array da ordinare e come indici 0 e n-1 (dove n indica la lunghezza dell'array).
Si passa come estremo destro l'indice dell'effettiva ultima posizione perchè l'algoritmo itera in un intervallo del tipo [ 0 ; array.length ), che si può scrivere equivalentemente come [0 ; array.length-1 ] semplificando i controlli nei vari cicli.
Cenni sulla complessità
Complessità del processo di fusione
La complessità del processo di fusione ha crescita lineare, infatti ad ogni iterazione la dimensione dell'array finale cresce sempre di 1. E' quindi O(N).
C'è però un costo iniziale pari a O(N) per la copia del vettore di appoggio.
Costo dell'algoritmo
T(n) = 2T(n/2) +
Mediante opportuni passaggi algebrici è possibile giungere alla conclusione che la complessità dell'algoritmo è pari a .
Quando è utile Merge Sort?
Merge Sort risulta particolarmente utile quando si ha a che fare con Linked List proprio perchè l'inserimento ha complessità lineare. Siccome i nodi della lista non sono adiacenti, è particolarmente comodo utilizzare questo algoritmo.