Hashmap con Concatenamento: hashing, collisioni e prime funzioni

Hashing con metodo della divisione, moltiplicazione e hashing per stringhe. Inserimento, ricerca e cancellazione in una hashmap.

Oggi andremo a vedere dei concetti strettamente legati alle hashmap. I concetti che andremo a vedere sono quelli di hashing e collisioni.

Hashing

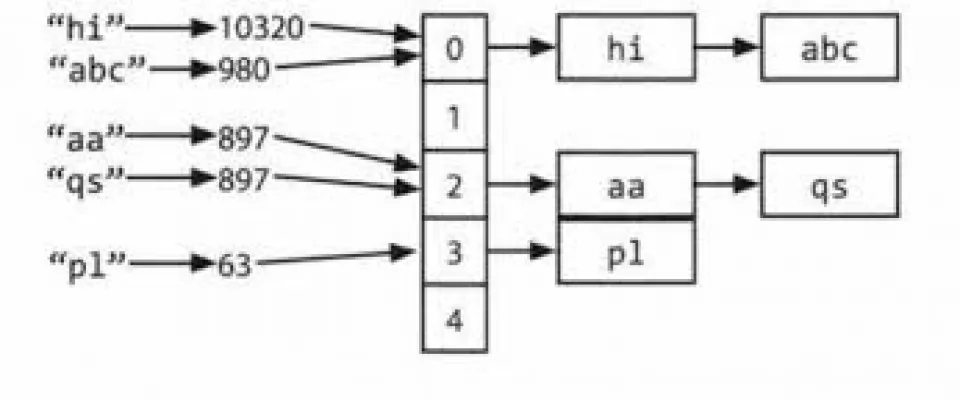
L'idea dell'hashing con concatenamento è quella di creare una sorta di array di liste, all'interno del quale, in qualche modo, inserire gli elementi.

Abbiamo bisogno di mappare le chiavi di ogni nodo per capire in quale posizione dell'array inserirlo.

La posizione della chiave k è determinata attraverso una funzione:

h: U --> {0, ..., m-1}

dove U è l'universo dei dati rappresentati ed m è la dimensione dell'array.

Questa funzione è detta funzione di hash.

Esempi di funzioni di hash

Hashing su stringhe

Un modo molto semplice di fare hashing su chiavi di tipo stringa è quello di considerare i codici ASCII e di farne la somma "pesata", utilizzando come base 128. Vediamo meglio, usando la parola "oca" come esempio.

oca --> 111 · 128^2 + 99 · 128^1 + 97 · 128^0

Questa procedura ricorda un po' la procedura di conversione in decimale da una base b.

Metodo della divisione

Il metodo della divisione è il metodo di hashing che richiede meno sforzo implementativo, ma che a livello prestazionale non offre prestazioni di un gran livello. Il vantaggio a livello accademico è che non richiede molto codice per funzionare. 

La funzione è la seguente: 

h(k) = k mod m

dove k è la chiave da mappare ed m è la dimensione dell'array all'interno del quale mappare le chiavi.

Metodo della moltiplicazione

Il metodo della moltiplicazione consiste nel calcolare il prodotto: 

h(k) = floor(m * (kA - floor(kA)))

A è un numero reale. E' stato dimostrato che una buona approssimazione di A è A = (sqrt(5)-1)/2 = 0.6180339887.

Implementazione di una funzione di hash 

Vediamo ora in che modo è possibile implementare la funzione di hash con il metodo della divisione in C.

Header file

int hash_with_div_int(int *key, int size);

La funzione prende come parametro un puntatore ad intero, che rappresenta la chiave da mappare e la dimensione dell'array all'interno del quale mappare la chiave.

Implementazione

int hash_with_div_int(int *key, int size){
  return *key % size;
}

Questa funzione implementa esattamente il metodo della divisione spiegato prima. C'è bisogno di dereferenziare il puntatore perchè il modulo viene calcolato rispetto al valore della chiave e non rispetto all'indirizzo.

Collisioni

La tecnica dell'hashing con concatenamento ha diversi vantaggi, ma allo stesso tempo porta alla luce un problema che è indispensabile gestire.

• riduciamo lo spazio utilizzato
• perdiamo la diretta corrispondenza fra chiavi e posizioni
• m < |U| e quindi inevitabilmente possono esserci delle collisioni

Per collisione intendiamo il fatto che due chiavi possano essere mappate nella stessa posizione. 

Ipoteticamente, dovendo mappare con il metodo della divisione le chiavi 10 e 110 avendo m = 100, entrambe verranno mappate nella posizione 10.

Esiste un concetto teorico che idealmente permetterebbe di non avere collisioni. Il concetto è quello di hashing perfetto.

Hashing perfetto

Una funzione di hash si dice perfetta se non crea mai collisioni. Formalizzando l'idea abbiamo che:

k1 ≠ k2 ⇒ h(k1) ≠ h(k2)

Questo è un concetto puramente teorico.

Concatenamento

Il concatenamento è il meccanismo con cui gestiamo le collisioni. Significa che, al posto di inserire un elemento per ogni posizione dell'array, concateniamo in una lista tutti gli elementi che generano collisione. 

Questa tecnica permette di gestire in maniera efficiente le collisioni. Le operazioni di inserimento vengono fatte in tempo costante, dal momento in cui, come ho mostrato nell'articolo sulle liste di trabocco, viene mantenuto il puntatore sia alla testa che alla coda.

Uniformità semplice

Un altro concetto fortemente legato all'hashing è il concetto di uniformità semplice. 

Dire che una funzione di hash gode della proprietà di uniformità semplice significa che la funzione h distribuisce i valori in modo uniforme tra le celle. 

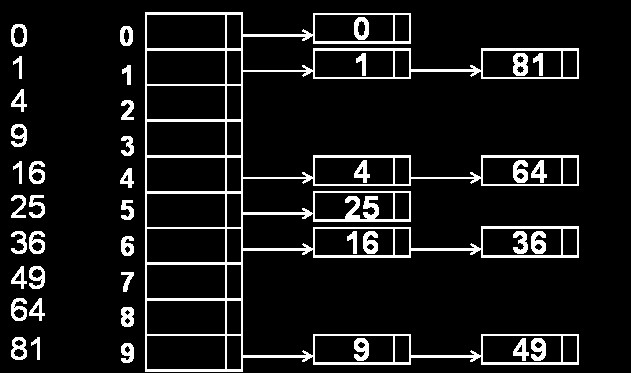
Esempio

U = {00, 01, ..., 99}

m = 10

h(k) = k mod 10

Questa funzione gode della proprietà di uniformità semplice perchè ogni valore compare esattamente dieci volte ed ogni cella è destinazione di dieci chiavi.

Implementazione delle tabelle hash

Creazione di una nuova hashmap

hashmap *create_new_map(int s){
  hashmap *map = (hashmap*)malloc(sizeof(hashmap));
  map -> items = (overflow_list**)malloc(s*sizeof(overflow_list*));
  for(int i = 0; i < s; i++){
    map -> items[i] = create_empty_doubly_linked_list();
  }
  map -> size = s;
  return map;
}

Questa funzione funge da costruttore per una nuova hashmap. Quindi, dopo aver allocato un puntatore per la mappa, si alloca lo spazio necessario per contenere le liste di trabocco, riservando sufficiente spazio per tante liste quante il parametro s.

Dopodichè si inizializzano tutte le liste come liste vuote, usando l'apposita funzione scritta per le liste doppiamente concatenate.

Inserimento di una nuova associazione

Come per ogni struttura dati, c'è la necessità di effettuare operazioni di inserimento. In questo particolare caso, la caratteristica è che non vogliamo elementi duplicati, per cui la complessità dell'inserimento è più alta rispetto a quella dell'algoritmo presentato nelle liste di trabocco. Questo perchè l'inserimento è accompagnato da una ricerca della chiave.

void insert_association(hashmap *map, void *key, void *val,
HASHFUNC hash,CMPFUNC compare){
     int i = hash(key, map->size);
     node_t *list = map -> items[i] -> head;
     if(contains_key(list, key, compare)==NULL)
      insert_item(map->items[i], key, val);
}

La cosa importante è che tra i parametri abbiamo la funzione di hash e una funzione di comparazione.

Questi due parametri ci servono proprio per effettuare le operazioni di ricerca, inserimento e calcolo dell'indice.

Estrazione del valore data una chiave

void *retrieve_value(hashmap *map, void *key,
HASHFUNC hash, CMPFUNC compare){

  int i = hash(key, map->size);
  node_t *retrieved;
  node_t *h = map -> items[i] -> head;
  retrieved = contains_key(h, key, compare);
  return retrieved != NULL ? retrieved -> data : NULL;

}

Questa funzione permette di recuperare il valore memorizzato in un nodo data la sua chiave. Calcoliamo quindi la posizione dell'array all'interno della quale si dovrebbe trovare la nostra chiave. 

Dopodichè si effettua la ricerca e, in base all'esito, si restituisce NULL se la chiave non è stata trovata, il campo data altrimenti.

Con questa tecnica, la ricerca in una hashmap si riduce ad una ricerca in una lista di trabocco, algoritmo che già conosciamo.

Rimozione di un'associazione da una hashmap

L'ultimo algoritmo fondamentale da conoscere è quello di rimozione di un'associazione. 

void delete_association(hashmap *map, void *key,
HASHFUNC hash, CMPFUNC compare){
  if(map != NULL){
    int i = hash(key, map->size);
    remove_item(map->items[i], key, compare);
  }
}

Qui, se la mappa non è nulla, calcoliamo la posizione dell'array all'interno della quale cercare l'elemento e successivamente l'algoritmo da eseguire è quello di rimozione in una lista di trabocco.

Possiamo vedere come anche qui l'eliminazione si possa ridurre alla cancellazione in una lista, richiedendo così uno sforzo implementativo praticamente nullo.

Spero che questa lezione sulle hashmap sia piaciuta. Vi invito ad implementare personalmente il codice che propongo e chissà, magari avrete qualche suggerimento. 

Alla prossima 

Alessio Mungelli

Computer Science student at UniTo (University of Turin), Network specializtion, blogger and writer. I am a kind of expert in Java desktop developement with interests in AI and web developement. Unix lover (but not Windows hater). I am interested in Linux scripting. I am very inquisitive and I love learning new stuffs.