Welcome back to this overview about the Java world! Today, we are going to talk about a renowned sorting algorithm: the Quick Sort.
The Quick Sort is not very suitable for educational purposes because its implementation may not be trivial, but at the performance level it offers some advantages that are not indifferent, unlike the previously trated Bubble Sort.
Let's try to understand better what is Quick Sort.
First of all, let's see an image that gives us an idea of how the algorithm works.
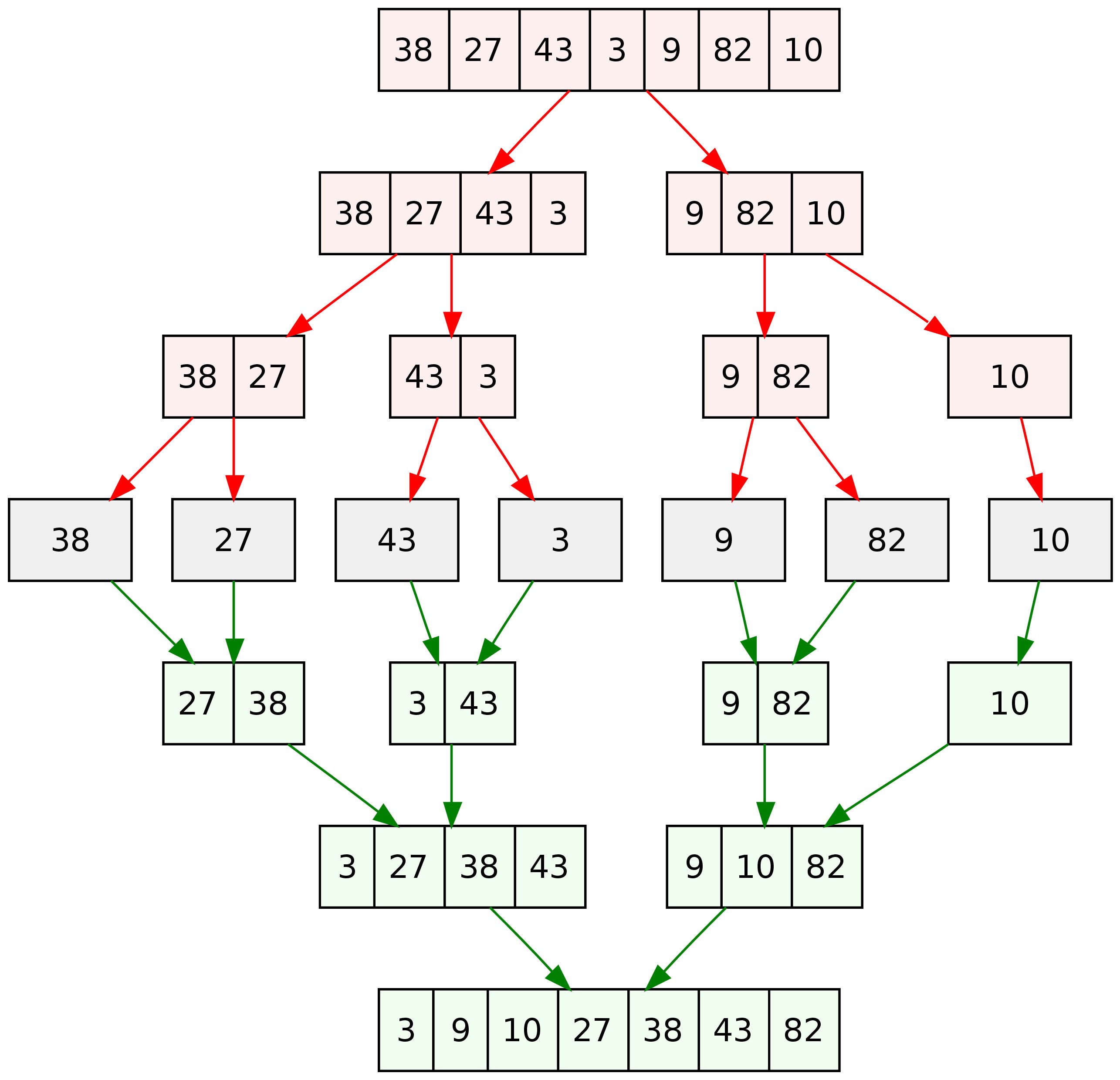
Foundamental features and description
The Quick Sort is one of the most used algorithms, expecially when huge amounts of data have to be treated. Just like some other algorithms, it is part of the Divide and Conquer family.
It means that the processing is not done on the entire data collection, but it is recursively done on finite subsets of the collection. This feature makes the sorting operations lighter from the moment that the values that have to be compared are two at most.
Let's remember that the Quick Sort is a stable and in-place algorithm. Generally no algorithm is stable, but it can be made stable using indexes as meter of comparison.
These are the main steps of the algorithm.
If the collection is composed of zero or one element, then it is sorted. Otherwise the following steps are performed:
- A pivot is chosen;
- The elements of the array are divided into two parts: the one of the elements before the pivot and the one of the elements after the pivot;
- The elements are sorted recursively repeating the 1 and 2 steps;
Implementation
import java.util.*;
public class QuickSort
{
/*
This function takes the last element as pivot,
place the pivot element in its right position
in the sorted array. It also puts every element smaller than the pivot
on the left and every element bigger than the pivot on the right.
*/
private static int partition(int arr[], int low, int high)
{
int pivot = arr[high];
int index = (low-1); // index of the smaller element. -1 at the beginning
for (int j=low; j<high; j++)
{
// if the current element is smaller than pivot
if (arr[j] < pivot)
{
index++;
// swap arr[index] and arr[j]
int temp = arr[index];
arr[index] = arr[j];
arr[j] = temp;
}
}
// swap arr[index+1] and arr[high] (or pivot)
int temp = arr[index+1];
arr[index+1] = arr[high];
arr[high] = temp;
return index+1;
}
/* The main function that implements QuickSort()
arr[] --> array to be sorted,
low --> starting index,
high --> ending index */
public static void sort(int arr[], int low, int high)
{
if (low < high)
{
/* pi is the partitioning index, arr[pi] is now in the right place */
int pi = partition(arr, low, high);
// Recursively order the elements before
// partition and after partition
sort(arr, low, pi-1);
sort(arr, pi+1, high);
}
}
// Driver program.
public static void main(String args[])
{
int arr[] = {10, 7, 8, 9, 1, 5};
int n = arr.length;
QuickSort.sort(arr, 0, n-1);
System.out.println("sorted array");
System.out.println(Arrays.toString(arr));
}
}
Let's understand the code
The most important element is the choice of the pivot. The ideal pivot should be the medium element of the collection but it is too difficult to find in an unsorted collection. The choices can be different. The first element, the last element, the middle element or a random element can be chosen as pivot.
The main method is partition that takes as parameters the collection to sort, that is an array of integer numbers, and the two extremes of the array, low and high.
In this method every swapping operation is done. This is the method that implements the majority of the algorithm.
The method's body contains simply some swapping operations done only under certain conditions. The very easy principle is the one that exchanging two sorted elements is useless, so the current element j is compared to the pivot.
The indexes have the following meanings:
- index stands for the minimum element that has been examined;
- j is the current element;
The sort method is the wrapper for partition. The control on low and high is performed in order to verify that they "make sense" and that situations where low=2 and high=1 don't occurr since inconsistent situations can happen.
The partition index is calculated.
At the end we have the main method, where the array to sort is created. Then the sort method is called on the array with 0 and n-1 as indexes (where n is the array's length).
Must be precised that I chose to make the sort method static. I decided to implement it as a static method because I imagined the code presented above as a part of a bigger class that implements more than one algorithm. Since sort is static, partition must be static.
A non-static method could have been implemented and the effect would have been the same.
Clearly, just like the majority of the situations that happen in Computer Science, there are many different variations of the implementation of the Quick Sort. Every variant has the same final result. The implementation details change.
Hints about complexity
The time taken from the Quick Sort can be expressed as:
T(n) = T(k) + T(n-k-1) +(n)
The first two terms represent the two recursive calls and k stands for the element "smaller" than the pivot. The effective time depends on the pivot choice. Let's look at some particular cases:
Worst case:
T(n) = T(n-1) +(n)
It happens when the smallest or the biggest element is chosen as pivot.
The complexity can be written as (n2). Notice the exponential growth.
Best case:
T(n) = 2T(n/2) +(n)
The complexity can be written as (nLogn).
Average case:
T(n) = T(n/9) + T(9n/10) +(n)
In order to make an accurate analysis of the complexity in the average case we should calculate every possible permutation of the elements of the collection and it is not easy. We can have an idea of the complexity considering the case where partition puts O(n/9) elements in a subset and O(9n/10) in the other subset.
The complexity can be written as (nLogn) also in this case.
Curiosity: what is three-way-quick-sort?
Il three-way-quick-sort è una versione del Quick Sort dove la collezione da ordinare viene divisa così come segue:
The three-way-quick-sort is a version of the Quick Sort where the array to sort is divided as shown below:
- array[low...i] is the subset of the elements smaller than the pivot;
- array[i...j-1] is the subset of the element equals to the pivot;
- array[j...high] is the subset of the element bigger than the pivot;
E' evidente che questa versione sia conveniente solo quando ci sono diversi elementi ridondanti nella collezione. In caso contrario sarebbe priva di senso.
Clearly this version has to be used only if there are many redundant element in the collection. In the other case it would not make any sense.

