Programmando, nasce spesso la necessità di ordinare le collezioni di dati o oggetti che devono poi essere manipolate. Ordinare una lista può essere utile nei casi in cui si debbano fare ricerche molto rapide. Vedremo più avanti quanto mantenere una lista ordinata sia utile per effettuare ricerche dicotomiche e avere quindi i risultati in un tempo nettamente minore rispetto ad una ricerca sequeziale.
Nel corso dell'articolo faremo riferimentro per la maggior parte del tempo ad array di interi. L'algoritmo è lo stesso nel caso in cui il tipo sia diverso.
Proprietà degli algoritmi
Questo è un discorso che farò ora e vale per tutti gli algoritmi di ordinamento di cui andremo a parlare nei prossimi articoli.
Generalmente, tutti gli algoritmi di ordinamento godono di proprietà utili a studiarli e soprattutto, per decidere quale sia il più consono alla situazione che si è presa in esame. Vediamo meglio.
Stabilità
Un algoritmo di ordinamento si dice stabile se preserva l'ordine relativo dei dati con chiavi uguali all'interno del file da ordinare. Ad esempio, se abbiamo in esame una lista di persone ordinate in ordine alfabetico, un algoritmo stabile restituirà sempre una lista ordinata in ordine alfabetico. Se l'algoritmo fosse instabile, si otterrebbe una lista senza alcuna traccia dell'ordinamento precedente.
Un possibile modo di forzare la stabilità dell'algoritmo è quello di aggiungere una chiave univoca ad ogni elemento. Questo principio viene ripreso anche in ambito database.
Sul posto o in-place
Un algoritmo si dice in-place se utilizza un numero costante di variabili per ordinare l'array e non usa array di supporto.
Adattività
Un algoritmo si definisce adattivo quando trae vantaggio dagli elementi già ordinati.
Andiamo ora ad analizzare in dettaglio alcune implementazioni di un algoritmo di ordinamento: il Bubble Sort.
Bubble Sort
Il bubble sort è un algoritmo di ordinamento di per sè non molto efficiente, utilizzato spesso a scopi didattici per introdurre il concetto di algoritmo di ordinamento.
Perchè "bubble sort"?
Il nome dell'algoritmo deriva dal suo comportamento. Infatti gli elementi del vettore si comportano esattamente come le bollicine in un calice di champagne: le più grandi salgono verso l'alto mentre quelle più piccole rimangono in basso, esattamente come mostra la gif qui sotto.
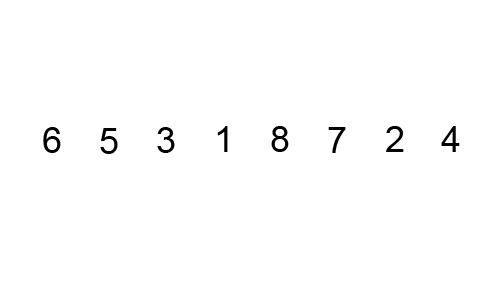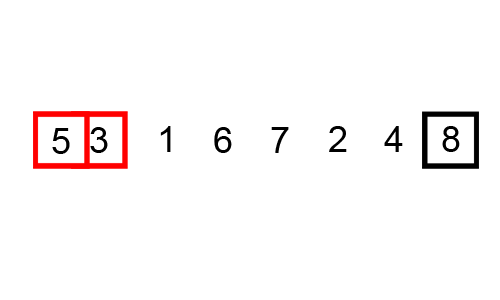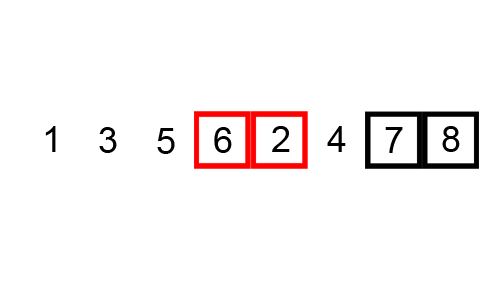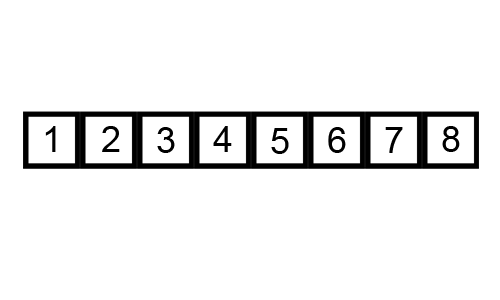
Flow-chart
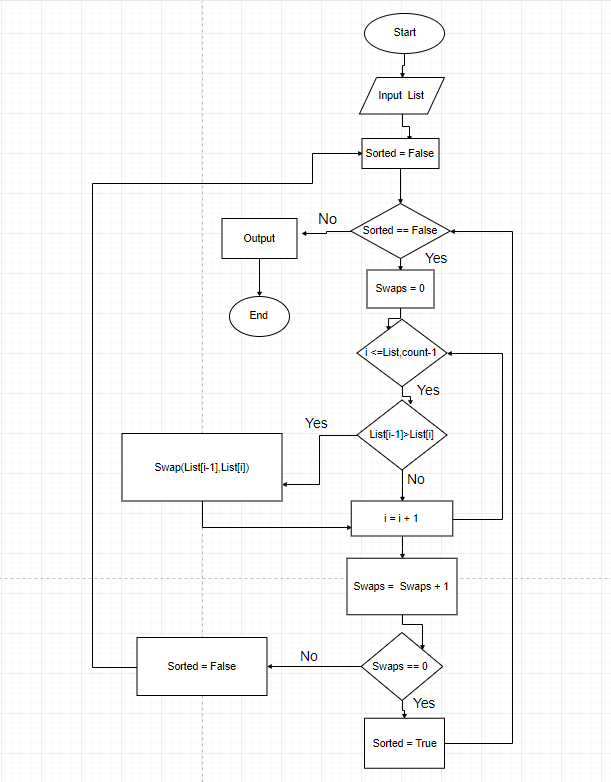
Implementazione
Precisiamo che il flow chart presenta una versione ottimizzata dell'algoritmo, mentre il codice qui sotto presenta la versione classica.
public static void bubbleSort(int[] v) {
int n = v.length;
int temp = 0;
for(int index=0; index < n; index++){
for(int j=1; j < (n-index); j++){
if(v[j-1] > v[j]){
//scambia elementi
temp = v[j-1];
v[j-1] = v[j];
v[j] = temp;
}
}
}
}
Questa implementazione iterativa mostra esattamente il procedimento mostrato dalla gif. Infatti, andando a stampare passo passo i vari stati dell'array durante il processo di ordinamento, otterremo:
[6, 5, 3, 1, 8, 7, 2, 4]
[5, 3, 1, 6, 7, 2, 4, 8]
[3, 1, 5, 6, 2, 4, 7, 8]
[1, 3, 5, 2, 4, 6, 7, 8]
[1, 3, 2, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]
Notiamo come il numero di passaggi che si devono fare per ordinare un array relativamente piccolo come quello dell'esempio sia veramente alto. Proprio per questo il bubble sort viene utilizzato fondamentalmente a scopi didattici a causa della sua inefficcienza. Proprio grazie alla predisposizione all'uso didattico, andiamo a fornire un'implementazione ricorsiva dello stesso algoritmo, definendo con swap il metodo che scambia due posizioni di uno stesso array.
//metodo ricorsivo per implementare il bubble sort su un sottoarray
public static void bubbleSort(int[] v, int n)
{
for (int index = 0; index < n - 1; index++) {
if (arr[index] > arr[index + 1]) {
swap(arr, index, index + 1);
}
}
if (n - 1 > 1) {
bubbleSort(arr, n - 1);
}
}
Il risultato ottenuto è lo stesso, ma cambia il modo in cui viene implementato.
Proprietà
Riprendendo il discorso sulle proprietà fatto in precedenza, possiamo tentare di identificare quali siano le proprietà del bubble sort.
Il bubble sort è stabile, infatti restituisce sempre un array ordinato crescentemente o decrescentemente indipendentemente dai dati presenti nella collezione.
E' in-place in quanto non utilizza array aggiuntivi per l'ordinamento.
E' adattivo, infatti nel caso in cui degli elementi siano ordinati, non effettua alcuna operazione e li lascia ordinati. Questa caratteristica permette di risparmiare un notevole numero di iterazioni.
Complessità
Facendo un discorso un po' più matematico, andiamo a vedere qualcosa sulla complessità dell'algoritmo. Facciamo una piccola premessa. La complessità si indica mediante i cosiddetti simboli di Landau, usati per paragonare l'andamento di due funzioni. Infatti si tende ad associare la complessità di un algoritmo ad una funzione, per poi paragonarla ad una nota.
Assumendo che la complessità di uno scambio sia O(1), la complessità dell'algoritmo è data dalla complessità dei cicli for annidati.
Nel caso migliore abbiamo una complessità pari a T(n)=n(n-1)/2 —> O(N²) mentre nel caso migliore l'array è già ordinato e quindi il numero di iterazioni è pari a 1.
Mediamente effettua circa N2 / 2 confronti ed altrettanti scambi.
Ottimizzazioni e conclusioni
Un primo modo di ottimizzare l'algoritmo si basa sul fatto che, se in una data iterazione n non si effettuano scambi, significa che l'array è ordinato e quindi l'algoritmo può terminare. Si fa ricorso quindi ad una variabile booleana che verifichi proprio questa condizione. Questo tipo di ottimizzazione è presentata nel flow chart sopra.
Una seconda linea di pensiero sostiene che se una data iterazione non sposta nessun elemento di posizione maggiore di un dato valore i, allora si può facilmente dimostrare che nessuna iterazione successiva eseguirà scambi in posizioni successive a tale valore i. L'ottimizzazione consiste nel memorizzare l'indice dove si è effettuato l'ultimo scambio e scandendo l'array fino a tale posizione. Anche questa tecnica evidentemente introduce un piccolo overhead.
Concludendo il discorso, possiamo dire che l'algoritmo si presta bene a fini didattici come detto prima. Non si presta bene ad ordinare array di grandi dimensioni.
Spezzando una lancia a suo favore, è facile da capire e implementare, non richiede un grande ammontare di memoria e la cosa più importante è che, una volta finito l'ordinamento, i dati sono pronti per l'elaborazione.

