Andiamo oggi ad analizzare in dettaglio un algoritmo di ordinamento non molto efficiente ma piuttosto utilizzato in diversi ambiti. Stiamo parlando del Selection Sort.
Vediamo meglio in dettaglio.
Intuizione
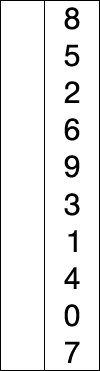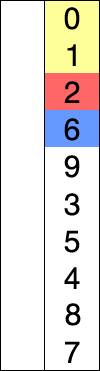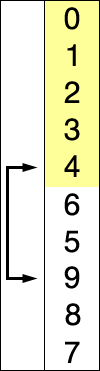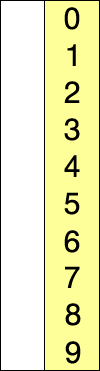
L'idea alla base è quella di suddividere l'array da ordinare in due sotto-array. Uno che contiene i dati già ordinati e occupa le prime posizioni dell'array mentre l'altro contiene i dati da ordinare e occupa tendenzialmente le posizioni finali dell'array. Inizialmente la sottosequenza di elementi ordinati è vuota mentre la sottosequenza di elementi non ordinati rappresenta l'intero array.
L'algoritmo sceglie ad ogni iterazione il minimo nella sottosequenza non ordinata e lo piazza nella sottosequenza ordinata. Il tutto va avanti sino a quando la sottosequenza di elementi non ordinati contiene ancora elementi.
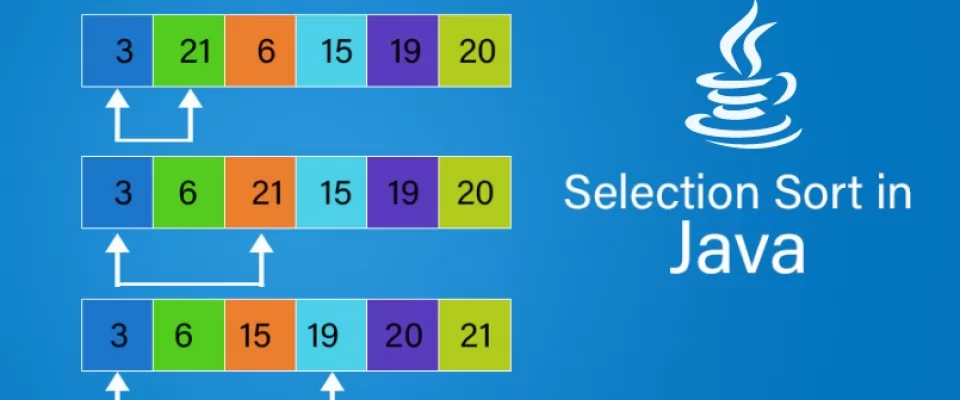
Vediamo meglio con una GIF:
Flow-chart
Andiamo ad analizzare il flow-chart dell'algoritmo, fornito gentilmente dagli amici di GeeksforGeeks.com.
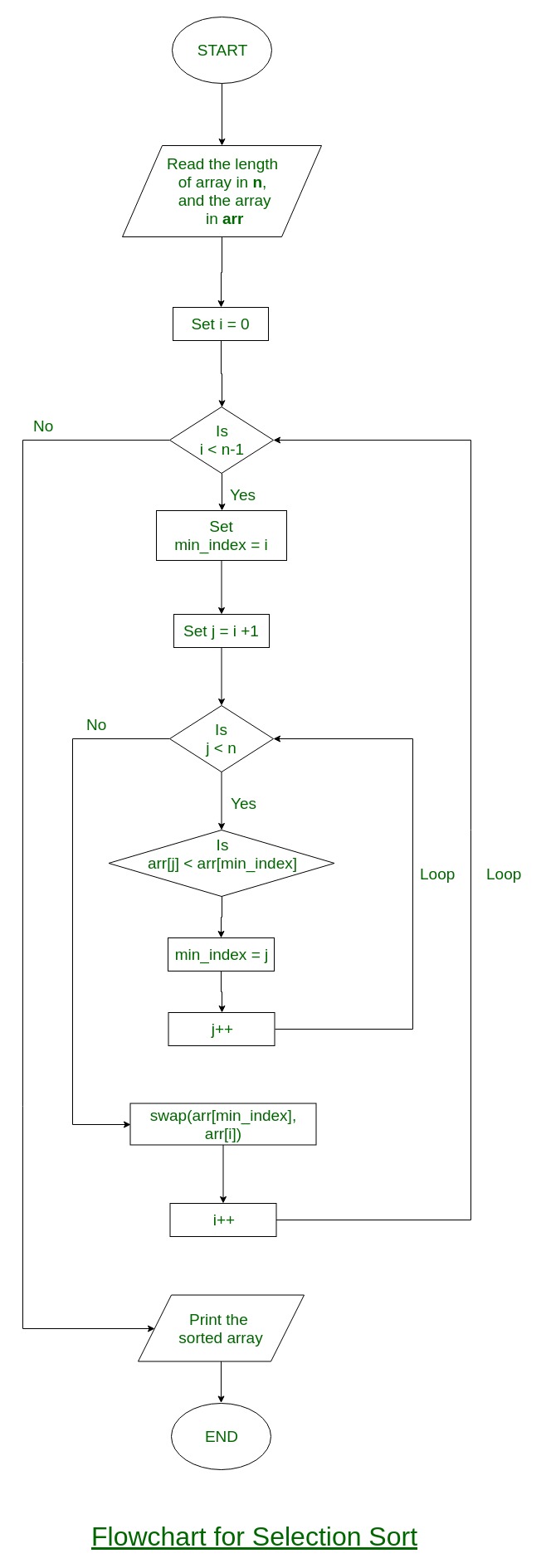
Abbiamo due cicli fondamentali che implementano l'intera procedura. Il primo ciclo serve a tenere traccia della posizione in cui inserire il minimo che abbiamo trovato mentre il secondo serve appunto a trovare il minimo all'interno della collezione.
Implementazione
Andiamo a vedere l'implementazione dell'algoritmo.
// Java program for implementation of Selection Sort
public class SelectionSort
{
public static void sort(int arr[]) {
int n = arr.length;
for (int index = 0; index < n-1; index++)
{
// Trova il minimo elemento in un array non ordinato
int min_idx = index;
for (int j = index+1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
// Scambia il minimo elemento trovato con
// il primo elemento
int temp = arr[min_idx];
arr[min_idx] = arr[index];
arr[index] = temp;
}
}
public static void main(String args[]){
int arr[] = {64,25,12,22,11};
System.out.println("Unsorted array");
System.out.println(Arrays.toString(arr));
SelectionSort.sort(arr);
System.out.println("Sorted array");
System.out.println(Arrays.toString(arr));
}
}
Capiamo il codice
Come negli esempi precedenti, il metodo di ordinamento è stato reso statico. Il primo ciclo serve a tenere traccia della posizione corrente del vettore mentre il ciclo più interno viene utilizzato per la ricerca del minimo.
Notiamo come la ricerca del minimo debba essere sequenziale, in quanto non ci sono i presupposti per poter effettuare una ricerca dicotomica, ad esempio.
Analizziamo in dettaglio i cicli che compongono l'algoritmo.
- ciclo esterno da 0 ad arr.length-1: questo ciclo tiene traccia delle effettive iterazioni della procedura, permettendo anche di tracciare la posizione in cui si dovrà mettere il nuovo minimo trovato. La cosa "interessante" è che si itera sino alla penultima posizione del vettore. La motivazione è alquanto banale. Quando si giunge all'ultima posizione, non ci sono più elementi con cui scambiarla, per cui è inutile effettuare un giro in più. E' sufficiente fermarsi alla penultima posizione;
- ciclo interno: questo ciclo serve a ricercare il minimo in una sottoporzione di array, nello specifico da index+1 ad arr.length-1. A differenza del ciclo esterno, qui si esamina anche l'ultima posizione in quanto è una possibile candidata come minimo. Non memorizziamo il valore del minimo ma bensì l'indice che ci servirà poi per lo scambio.
C'è infine la proedura di scambio, su cui vale la pena spendere qualche parola.
Ad un occhio poco esperto, la variabile temp potrebbe sembrare inutile. Al contrario, è indispensabile, perchè ci permette di non perdere il valore di una delle due variabili dopo la prima operazione di assegnamento. Infatti, prima si salva in temp il valore di array[min_idx], successivamente si piazza in array[min_idx] array[index[ e infine in array[index] si piazza temp. In questa maniera si scambiano due variabili correttamente.
Implementazione ricorsiva
// Recursive Java program to sort an array
// using selection sort
public class RecursiveSelectionSort
{
// restituisce l'indice del minimo
static int minIndex(int a[], int index, int j)
{
if (index == j)
return index;
// Trova il minimo degli elementi rimanenti
int k = minIndex(a, index + 1, j);
// Return minimum of current and remaining.
return (a[index] < a[k])? index : k;
}
// Selection sort ricorsivo. n è la lunghezza di a[] e index
// è l'indice dell'elemento iniziale.
public static void recurSelectionSort(int a[], int n, int index)
{
// Return when starting and size are same
if (index == n)
return;
// calling minimum index function for minimum index
int k = minIndex(a, index, n-1);
// scambio quando index e l'indice del minimo non sono gli stessi
if (k != index){
// scambio
int temp = a[k];
a[k] = a[index];
a[index] = temp;
}
// Chiamo ricorsivamente il metodo per il selection sort
recurSelectionSort(a, n, index + 1);
}
public static void main(String args[])
{
int arr[] = {3, 1, 5, 2, 7, 0};
System.out.println("Unsorted array");
System.out.println(Arrays.toString(arr));
// Chiamo la funzione
recurSelectionSort(arr, arr.length, 0);
System.out.println("Sorted array");
System.out.println(Arrays.toString(arr));
}
}
Capiamo il codice
Questo algoritmo si presta discretamente bene ad un'implementazione ricorsiva. Analizziamola in dettaglio.
- metodo minIndex: ha come parametri i due estremi all'interno dei quali è necessario ricercare il minimo. Il caso base è quando si arriva alla fine degli elementi da esaminare, per cui si restituisce l'indice corrente. L'ultima istruzione serve proprio a confrontare a[index] e a[k] e a restituire il minimo tra di loro.
- metodo recurSelectionSort: Il metodo ha come parametri l'array da ordinare e due numeri interi n e index, che rappresentano rispettivamente la lunghezza dell'array e la posizione che stiamo esaminando.
Il procedimento messo in atto è analogo a quello presentato nella versione iterativa. Trovo il minimo e lo scambio con la posizione corrente. Il minimo viene trovato ricorsivamente come spiegato prima. Al posto di un ciclo, usiamo un'implementazione ricorsiva per poter scorrere l'array. Infatti, dopo aver effettuato lo scambio, si richiama ricorsivamente il metodo, ma incrementando il parametro index, che rappresenta la posizione attuale all'interno della quale mettere il minimo.
Il main è analogo a quello precedente, dove si passano al metodo come parametri l'array da ordinare, la sua lunghezza e 0 come indice corrente iniziale.
Cenni sulla complessità
l ciclo interno è un semplice test per confrontare l'elemento corrente con il minimo elemento trovato fino a quel momento (più il codice per incrementare l'indice dell'elemento corrente e per verificare che esso non ecceda i limiti dell'array). Lo spostamento degli elementi è fuori dal ciclo interno: il numero di scambi è pari a (dato che l'ultimo elemento non deve essere scambiato). Il tempo di calcolo è determinato dal numero di confronti.
L'ordinamento per selezione effettua confronti e, nel caso peggiore/migliore/medio, scambi.
La complessità di tale algoritmo è dell'ordine di

 (dato che l'ultimo elemento non deve essere scambiato). Il tempo di calcolo è determinato dal numero di confronti.
(dato che l'ultimo elemento non deve essere scambiato). Il tempo di calcolo è determinato dal numero di confronti. confronti e, nel caso peggiore/migliore/medio,
confronti e, nel caso peggiore/migliore/medio,  scambi.
scambi.